Interpreting the ultimate confusion Matrix in Machine Learning in 2023

As we all know ,in machine learning, the Classification model divides the data into categories. However, after training the model using  cleaned and pre-processed data, it is not easy to know if our classification model will produce the desired result. In such a situation, the Confusion matrix proves to be very useful. In this blog, let us explore the use of  confusion matrix in machine learning with example.

This blog will certainly help you achieve a better understanding about the confusion matrix in machine learning example. So, let us not get confused any more, rather, gain clarity about the confusion matrix! To gain more skills, knowledge and advancement in your career, read our another blog “Discover what are the skills required for machine learning in 2023“.

What Are Confusion Matrix in Machine Learning, and Why Do We Need Them?

A confusion matrix, also known as an error matrix, is a performance evaluation tool in machine learning that provides a summary of the predictions made by a classification model on a set of test data. It is commonly used to assess the performance of a classification algorithm in depth. We shall learn more about the confusion matrix in machine learning, further in the blog.

A confusion matrix helps in representing the various prediction outputs and results of a classification problem in the form of a table. Therefore, we can get a clear visualization of the outcomes. Using the matrix, a table can be plotted which depicts all the predicted.

Do you want to become a Machine Learning Engineer? Enroll Here

What is a 2X2 Confusion Matrix in Machine Learning examples?

Now that  you have got an overview of the confusion matrix, you would like to know more about what is confusion matrix with example. A 2×2 confusion matrix is a specific type of confusion matrix that is used when dealing with binary classification problems. It represents the performance of a machine learning model that classifies instances into two classes: positive and negative (or 1 and 0). In  the diagram below, we can see four different combinations of predicted and actual values of a classifier represented in the form of a 2X2 matrix. 

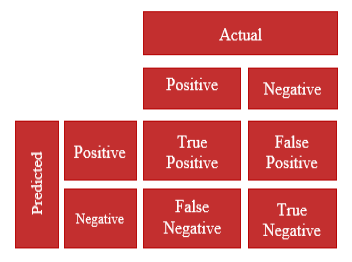
Here is what each cell of the matrix represents:

1. True Positive (TP): The number of instances that are actually positive and correctly predicted as positive by the model.
2. False Negative (FN): The number of instances that are actually positive but incorrectly predicted as negative by the model.
3. False Positive (FP): The number of instances that are actually negative but incorrectly predicted as positive by the model.
4. True Negative (TN): The number of instances that are actually negative and correctly predicted as negative by the model.

All the attributes explained above help us to understand the confusion matrix in machine learning with example, better. The 2×2 confusion matrix allows you to evaluate the performance of the model by calculating various metrics such as accuracy, precision, recall, and F1-score. These metrics can be derived from the values in the confusion matrix and provide insights into the model’s predictive power and potential weaknesses in binary classification tasks. An example for a 2X2 Confusion matrix given below:

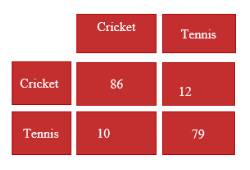
Let us consider a confusion matrix made for a classifier which classifies people based upon the attribute whether they like cricket or tennis. The values obtained are as follows:

True Positives (TP) = 86
True Negatives (TN) = 79
False Positives (FP) = 12
False Negatives (FN) = 10

Now, in order to understand how accurate the model is predicting, we need to use the following metrics:

1. Accuracy: Accuracy is a common confusion matrix in machine learning used to evaluate the overall performance of a classification model. It represents the proportion of correctly predicted instances(both true positives and true negatives) out of the total number of instances in the dataset. It is calculated using the formula: Accuracy = (TP +TN)/(TP + TN + FP + FN). In our example, Accuracy =(86 +79)/(86 + 79 + 12 + 10)= 0.8823= 88.23%
2. Precision: Precision measures the proportion of correctly predicted positive instances (true positives) out of all instances predicted as positive (true positives and false positives). It  focuses on the quality of positive predictions. It is calculated using the formula: Precision = TP/(TP + FP). In our example, Precision = 86/(86 + 12) = 0.8775 = 87.75%
3. Recall: Recall measures the proportion of correctly predicted positive instances (true positives) out of all actual positive instances (true positives and false negatives). It focuses on the model’s ability to capture all positive instances. Recall is calculated using  the formula: Recall = TP/(TP + FN). In our  example, Recall = 86/(86 + 10) = 0.8983 = 89.83%
4. F1-score: The F1-score is a metric that combines precision and recall into a single value, providing a balanced measure of a model’s performance. It is the harmonic mean of precision and recall and is calculated using the formula: F1-score =2 * Precision * Recall/(Precision + Recall). In our  example, F1-Score = (2* 0.8775 * 0.8983) / (0.8775 + 0.8983) = 0.8877 = 88.

Do you want to become a Machine Learning Engineer? Enroll Here

What is the Use of Confusion Matrix in machine learning?

The confusion matrix is a fundamental tool for evaluating the performance of a machine learning model, particularly in classification tasks. We have learnt that a confusion matrix summarises the prediction outcomes of a classifier model. Let us understand the use of confusion matrix in machine learning:

Here are some common uses of the confusion matrix in machine learning:

1. Accuracy Assessment: The confusion matrix in machine learning provides the performance metrics such as accuracy, precision, recall, and F1-score which help assess how well the model is performing and provide insights into its strengths and weaknesses. 
2. Model Selection: When comparing multiple models, the confusion matrix in machine learning can be used to compare their performance and choose the one that performs the best based on specific evaluation metrics. For example, you might prioritize models with high precision or recall, depending on the problem domain.
3. Error Analysis: By examining the values in the confusion matrix, you can identify the types of errors made by the model. This analysis helps you understand which classes are being misclassified and why.
4. Threshold Adjustment: In binary classification problems, the confusion matrix allows you to visualize the trade-off between true positive rate (recall) and false positive rate. By adjusting the decision threshold, you can control the balance between precision and recall based on your specific requirements.
5. Imbalanced Classes: The confusion matrix is particularly useful when dealing with imbalanced class distributions. It helps to identify whether the model is biased towards the majority class or struggling to detect instances of the minority class.
6. Model Monitoring: Once a model is deployed in a production environment, the confusion matrix can be used to monitor its performance over time. By regularly updating the confusion matrix with new predictions and evaluating the metrics, you can detect any degradation in performance or changes in the data distribution. 

Conclusion

To sum up our learnings regarding the confusion matrix in machine learning example, we can conclude that it is a tool to measure the performance of a classifier model.

Overall, the confusion matrix provides a comprehensive and concise summary of the model’s performance, enabling data scientists to make informed decisions about model selection, parameter tuning, and improvements. It allows us to identify the errors made by the model, which can guide further improvements in the model or data collection process. This blog has provided a good insight on what is the use of confusion matrix in machine learning.

To learn more about machine learning and its matrices to make your career as a machine learning engineer, you can join Win in life Academy. Register Now.